Οι εκπαιδευτικοί μπορούν να αξιοποιήσουν το ηλεκτρονικό εργαλείο της Μαθησιακής Ενότητας για να προβούν στο δικό τους σχεδιασμό μάθησης και να συνδυάσουν τις δραστηριότητες που επιλέγουν με τις Γνωστικές Διαδικασίες.
Υπάρχουν δύο πτυχές που αφορούν την τεκμηρίωση που επιτυγχάνεται με τη Μαθησιακή Ενότητα: μια προορατική/προκαταρτική (που αναφέρεται στο σχεδιασμό, και στα βήματα πριν τη διδασκαλία) και μια αναδρομική (που αναφέρεται στην αναδιατύπωση πρακτικών μετά τη διδασκαλία, και την καταγραφή των βέλτιστων πρακτικών σε μια τράπεζα γνώσης).
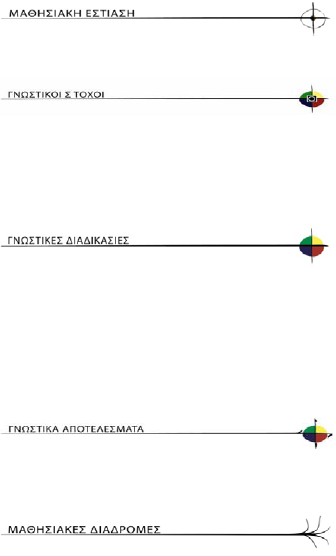
Ακολουθεί η συνολική αρχιτεκτονική της Μαθησιακής Ενότητας:
 |
|
|
|
Επιπλέον υπάρχουν δύο χώροι σχεδιασμού. Ο ένας χώρος ‘γράφεται’ στην επαγγελματική γλώσσα του εκπαιδευτικού (έτσι ώστε οι σχεδιασμοί μάθησης να μπορούν να γίνουν αντικείμενο ανταλλαγής μεταξύ συναδέλφων), και η άλλη πλευρά είναι γραμμένη απευθείας στη γλώσσα των μαθητών και της σχολικής τάξης (έτσι ώστε οι μαθητές να μπορούν να έχουν πρόσβαση σε μια Μαθησιακή Ενότητα παίρνοντας ένα σχετικά αυτόνομο ρόλο στη μάθηση τους):
- Ο σχεδιαστικός χώρος του εκπαιδευτικού (The Teacher Resource Space): Είναι ένα περιβάλλον σχεδιασμού προγραμμάτων σπουδών και διδακτικών ενοτήτων, μια ‘σκαλωσιά’ (scaffold) για το σχεδιασμό μαθησιακών διαδικασιών. Εδώ, δημιουργούνται οι σχεδιασμοί μάθησης χρησιμοποιώντας την επαγγελματική γλώσσα της εκπαίδευσης: διατύπωση στόχων, ανάπτυξη και αλληλουχία δραστηριοτήτων και οργάνωση της αξιολόγησης. Η Μαθησιακή Ενότητα φέρνει το σχεδιασμό μάθησης στο διαδικτυακό περιβάλλον του 21ου αιώνα. Παρέχει τεράστιες δυνατότητες «κοινωνικής δικτύωσης» για την ανταλλαγή διδακτικών σχεδίων μεταξύ εκπαιδευτικών, είτε πρόκειται για ένα μεμονωμένο συνάδελφο, είτε για τους εκπαιδευτικούς σε ένα σχολείο, είτε για άλλους συναδέλφους εκτός σχολείου. Οι εκπαιδευτικοί έχουν τη δυνατότητα να μοιραστούν Μαθησιακές Ενότητες με τους συναδέλφους στο δικό τους σχολείο και πέρα από αυτό, αλλά και να ανακαλύψουν και να ξαναχρησιμοποιήσουν Μαθησιακές Ενότητες με βάση το επίπεδο μάθησης, το μάθημα και το θέμα τους. Επίσης, μπορούν να προσαρμόσουν και να ξαναγράψουν Μαθησιακές Ενότητες άλλων, σεβόμενοι και αναγνωρίζοντας πάντα τους κανόνες πνευματικής ιδιοκτησίας των προηγούμενων συντακτών.
- Ο σχεδιαστικός χώρος για το μαθητή ( Learner Resource Space): Είναι ένας χώρος όπου το περιεχόμενο σπουδών μπορεί να συγκεντρωθεί από τους εκπαιδευτικούς για τη διδασκαλία στους μαθητές, άμεσα και παράλληλα με το υλικό που υπάρχει στο δικό τους χώρο. Εδώ, οι σχεδιασμοί μάθησης μεταφράζονται στη γλώσσα της σχολικής τάξης, επιτρέποντας αυτόνομη και ασύγχρονη (συμπληρωματικά στην καθοδηγημένη/ και σύγχρονη) πρόσβαση από μεμονωμένους μαθητές ή ομάδες μαθητών. Αυτό το περιεχόμενο μπορεί να αποτελείται από ένα ευρύ φάσμα πηγών, συμπεριλαμβανομένου του αρχικού υλικού που έχει εκπονηθεί από τους εκπαιδευτικούς, των συνδέσεων με ηλεκτρονικό/διαδικτυακό υλικό, του ενσωματωμένου πολυμεσικού περιεχομένου, των σαρώσεων αποσπασμάτων από συμβατικά κείμενα, κλπ.
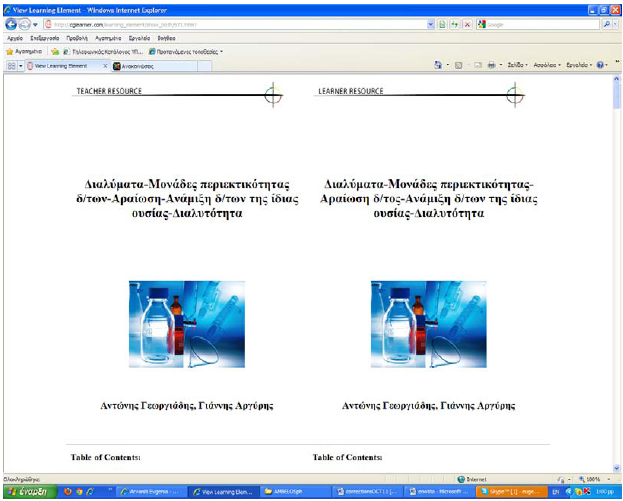
Παράλληλη Απόδοση των δύο σχεδιαστικών Χώρων: Η Οθόνη Προβολής μιας Μαθησιακής Ενότητας Προσχολικής Ηλικίας
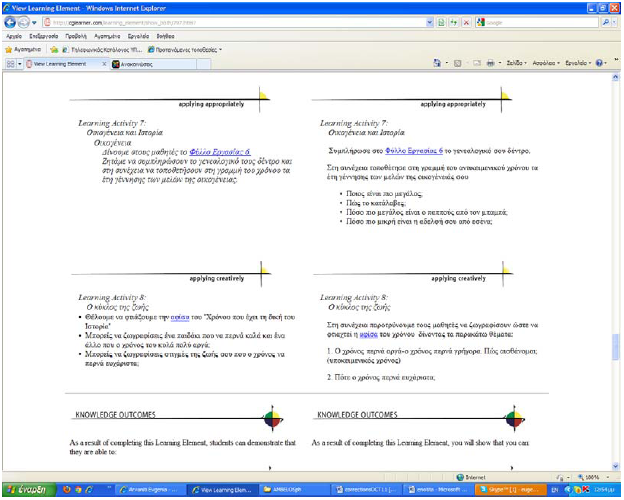
Παράδειγμα μιας μαθησιακής δραστηριότητας στη Μαθησιακή Ενότητα «Ο Τηλεπαρουσιαστής»
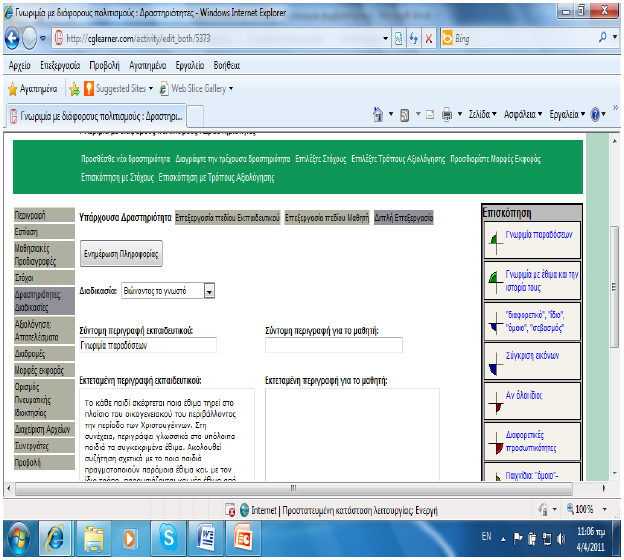
Ο Ηλεκτρονικός Χώρος Σχεδιασμού της Μαθησιακής Ενότητας
Η αξιοποίηση της Μαθησιακής Ενότητας μπορεί:
- Να εναρμονίσει τις διαδικασίες που τεκμηριώνουν τη μάθηση με τις σύγχρονες εφαρμογές κοινωνικής δικτύωσης Web «2.0» και τα ηλεκτρονικά μέσα επικοινωνίας και επικοινωνίας. Αυτό έχει πολλά εγγενή πλεονεκτήματα, όπως η ευκολία χρήσης, το χαμηλό κόστος, αλλά ίσως το πιο σημαντικό τη δυναμική πρόσβασης στο περιεχόμενο από εκπαιδευτικούς, μαθητές αλλά και τους ενδιαφερόμενους μετόχους σε κοινότητες μάθησης, όπως είναι οι γονείς. Με την προσβασιμότητα παγιώνεται η διαφάνεια και το άνοιγμα της πρόσβασης σε όποιο βαθμό γίνεται επιθυμητό από έναν μεμονωμένο εκπαιδευτικό ή σχολείο. Για παράδειγμα, οι εκπαιδευτικοί μπορούν να επιλέξουν να ανοίξουν τις διαδικασίες τους, ώστε και άλλοι συνάδελφοί τους να γνωρίζουν τι μαθαίνουν οι μαθητές τους. Παράλληλα, οι μαθητές μπορούν να δουν το σημείο εκκίνησης στη μάθησή τους και τη συνολική πορεία αυτής. Και οι γονείς μπορούν να έχουν συνεχή πρόσβαση στην συνολική επίδοση και πρόοδο των μαθητών.
- Να αναδειχθεί ο εκπαιδευτικός ως σχεδιαστής της μάθησης, και ως ειδικός εμπειρογνώμονας, μακριά από τον παραδοσιακό του ρόλο ως διαχειριστής/εκτελεστής του προγράμματος σπουδών και ως απλό μέσο μεταφοράς της διδακτέας ύλης. Επίσης, αναδεικνύει το σχολείο ως μια κοινότητα που παράγει γνώση. Για παράδειγμα, το μοντέλο της Μαθησιακής Ενότητας επιτρέπει στους εκπαιδευτικούς να δημιουργήσουν γενικές αλλά και τοπικές ερμηνείες των περιβαλλοντικών ή των ιστορικών ή των κοινωνικών επιστημών.
- Να μεριμνήσει για την ετερογένεια και τη διαφορετικότητα των μαθητών, επιτρέποντας πολλαπλή εξατομίκευση ή εκμάθηση σε μικρές ομάδες με ποικίλες μαθησιακές διαδρομές/επιλογές. Οι επιλογές αντλούνται από μια ηλεκτρονική τράπεζα διδακτικών ενοτήτων, στην οποία υπάρχει απευθείας πρόσβαση και σύνδεση με τον ίδιο το φάκελο εργασίας και σχεδιασμού Μαθησιακών Ενοτήτων του εκπαιδευτικού ή από μια ευρύτερη, ενοποιημένη τράπεζα Μαθησιακών Ενοτήτων, στην οποία συμμετέχουν πολλοί εκπαιδευτικοί. Με άλλα λόγια, οι Μαθησιακές Ενότητες αποτελούν μια πλούσια πηγή που υποστηρίζει μια στοχευμένη και διαφοροποιημένη μάθηση. Αυτό ενθαρρύνει επίσης τη δημιουργία ενός περιεχομένου που έχει άμεση σχέση με τις τοπικές κοινωνίες και που την ίδια στιγμή ευθυγραμμίζεται με τα επίσημα πρότυπα/προδιαγραφές του προγράμματος σπουδών.
- Να δημιουργήσει νέες ικανότητες σε ένα συγκεκριμένο πλαίσιο και μαθησιακά αποτελέσματα που θα αναμένουν περισσότερα πράγματα από το εκπαιδευτικό σύστημα, στο οποίο θα γίνεται πιο συνετή διαχείριση των διαθέσιμων εκπαιδευτικών πόρων. Οι εκπαιδευτικοί επανασχεδιάζουν παρόμοια εργαλεία, τόσο για τα καθημερινά σχέδια των μαθημάτων τους, όσο και για την προφορική συζήτηση στις τάξεις τους. Το μοντέλο της Μαθησιακής Ενότητας ζητά από τους εκπαιδευτικούς να εντάξουν τα σχέδια των μαθημάτων τους στη λογική μιας ψηφιακής εγγραφής. Αυτό απαιτεί περισσότερη δουλειά, σε πρώτη φάση, από ένα συμβατικό σχέδιο μαθήματος. Για το λόγο αυτό, οι εκπαιδευτικοί καταγράφουν μόνο τα καλύτερα τους σχέδια. Ωστόσο, η πρόσβαση στα σχέδια των άλλων συναδέλφων δημιουργεί τεράστιες δυνατότητες αποδοτικότητας και ανταλλαγής, καθώς ένας εκπαιδευτικός στο ίδιο σχολείο μπορεί να δημιουργήσει μια Μαθησιακή Ενότητα με μεγάλη τοπική σημασία, ή ένας άλλος εκπαιδευτικός σε ένα άλλο σχολείο μπορεί να δημιουργήσει ένα εξαιρετικό σχέδιο μαθήματος, το οποίο ένας τρίτος εκπαιδευτικός θα θέλει να ξαναγράψει ή να το προσαρμόσει στις δικές του τοπικές συνθήκες. Επίσης, επιτρέπει τη ρητή παρακολούθηση και τον αναστοχασμό σχετικά με τις εισροές των εκπαιδευτικών και τις εκροές των μαθητών, επιτρέποντας γρήγορες αναθεωρήσεις στον εκπαιδευτικό σχεδιασμό για πιο αποτελεσματικά και έγκαιρα αποτελέσματα.
- Να καλλιεργήσει μια κουλτούρα επαγγελματικής συνεργασίας. Το μοντέλο σχεδιασμού της Μαθησιακής Ενότητας υποστηρίζει την κοινή δημιουργία και συγγραφή, αλλά και την ομαδική διδασκαλία. Ενθαρρύνει τους εκπαιδευτικούς να μοιράζονται τις καλύτερες πρακτικές τους αναφορικά με το σχεδιασμό των προγραμμάτων σπουδών, αλλά και να ανταλλάσσουν με δυναμικό τρόπο τις επαγγελματικές τους γνώσεις. Το μοντέλο αυτό συνοδεύεται από τη δυνατότητα επιλογής ενός συμβατικού δικαιώματος πνευματικής ιδιοκτησίας ή μιας άδειας συλλογικής συγγραφής και ελεύθερης τεκμηρίωσης (Creative Commons). Και οι δύο επιλογές ενθαρρύνουν τον επανασχεδιασμό και την προσαρμογή των Μαθησιακών Ενοτήτων αναγνωρίζοντας τόσο τις αρχικές καταγραφές όσο και τις νέες εισφορές στο κείμενο.
- Να επιτρέψει τη συνεχή αξιολόγηση, τη λογοδοσία και τη λεπτομερή έκθεση των επιδόσεων. Η Μαθησιακή Ενότητα επιτρέπει στον εκπαιδευτικό να συσχετίσει και να συνδέσει με μεγάλη ακρίβεια το πρόγραμμα σπουδών και τους στόχους του (με υπερ-συνδέσμους αν είναι σε ηλεκτρονική μορφή ή με απλή παραπομπή) στην περιοχή των Γνωστικών Στόχων. Επίσης, παρέχει και ένα πεδίο Μαθησιακών Αποτελεσμάτων για συνεχή διαμορφωτική και τελική αξιολόγηση της επίδοσης των μαθητών.
Συνοπτικός Οδηγός Δημιουργίας μιας «Μαθησιακής Ενότητας»download
